The quantity
![]()
is a Killing tensor field for Friedmann-Lemaître-Robertson-Walker (FLRW) spacetime, which models a homogeneous and isotropic universe. We can use it to conveniently derive the cosmic redshift of photons, or decay of “peculiar velocity” for particles with mass. ![]() is the metric tensor,
is the metric tensor, ![]() is the “scale factor”, and
is the “scale factor”, and ![]() is the 4-velocity of observers comoving with the Hubble flow with components
is the 4-velocity of observers comoving with the Hubble flow with components ![]() in the usual coordinate choices.
in the usual coordinate choices.
The number:
![]()
is conserved along a geodesic worldline ![]() (more precisely,
(more precisely, ![]() is the tangent vector under some affine parameter). Such a conserved quantity exists because Killing tensors correspond to symmetries of spacetime.
is the tangent vector under some affine parameter). Such a conserved quantity exists because Killing tensors correspond to symmetries of spacetime.
We can evaluate
![]()
A photon has norm-squared ![]() , and energy
, and energy ![]() as measured by a Hubble observer (assuming you chose the affine parameter to give the 4-momentum). A massive particle has norm-squared
as measured by a Hubble observer (assuming you chose the affine parameter to give the 4-momentum). A massive particle has norm-squared ![]() , and Lorentz factor
, and Lorentz factor ![]() as measured by a Hubble observer (assuming the affine parameter is proper time). The usual results follow easily. In my view this the most elegant derivation.
as measured by a Hubble observer (assuming the affine parameter is proper time). The usual results follow easily. In my view this the most elegant derivation.
Note you can tweak some quantities, because multiplying a conserved quantity by a constant gives another conserved quantity, and the same applies for a Killing vector/tensor. So we may use the unnormalised scale factor ![]() in place of
in place of ![]() , because
, because ![]() is also a Killing tensor, with conserved quantity
is also a Killing tensor, with conserved quantity ![]() . As another example, for a timelike particle with constant mass
. As another example, for a timelike particle with constant mass ![]() , we may define
, we may define ![]() which is also conserved.
which is also conserved.
Curiously, the tensor contains the spatial projector ![]() for the Hubble observers. This is just the “space” part of the metric, along the usual homogeneous and isotropic spatial slices. We can rearrange the conserved quantity to give:
for the Hubble observers. This is just the “space” part of the metric, along the usual homogeneous and isotropic spatial slices. We can rearrange the conserved quantity to give: ![]() , then take the square root. In words, the length of the spatial part of the tangent vector is inversely proportional to the scale factor. More simply, Hubble observers measure things to lessen? (I need to think about the spatial geodesic case more…) These results sound familiar and unremarkable, but are rigorous and general.
, then take the square root. In words, the length of the spatial part of the tangent vector is inversely proportional to the scale factor. More simply, Hubble observers measure things to lessen? (I need to think about the spatial geodesic case more…) These results sound familiar and unremarkable, but are rigorous and general.
The only textbook I know which identifies it as a Killing tensor is Carroll (2004, §8.5)  . (However Wald (1984, §5.3a)
. (However Wald (1984, §5.3a)  deserves credit for using a Killing vector in the same fashion. See my forthcoming post on FLRW Killing vectors.) One source which gives the tensor is Maharaj & Maartens (1987a, §4)
deserves credit for using a Killing vector in the same fashion. See my forthcoming post on FLRW Killing vectors.) One source which gives the tensor is Maharaj & Maartens (1987a, §4)  and (1987b, §3)
and (1987b, §3)  . (While they identify the tensor, and the resulting conserved quantity which they interpret as linear momentum, the term “Killing tensor” is not mentioned.) Also there is similar content in much older sources, including Robertson & Noonan (1968)
. (While they identify the tensor, and the resulting conserved quantity which they interpret as linear momentum, the term “Killing tensor” is not mentioned.) Also there is similar content in much older sources, including Robertson & Noonan (1968)  .
.
The coordinate choice should not matter, as we can easily write the expression in a tensorial way. One can check that indeed ![]() , where the parentheses denote symmetrisation of the indices.)
, where the parentheses denote symmetrisation of the indices.)


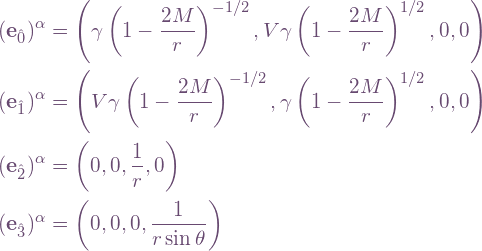
![Rendered by QuickLaTeX.com \[\fvec u_{\rm obs}=\left(\Schw^{-1/2},0,0,0\right)\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-492ec50d4e2d8170e1f27d344d1d02ba_l3.png)
![Rendered by QuickLaTeX.com \[u^\mu=\left(\gamma\Schw^{-1/2},V\gamma\Schw^{1/2},0,0\right)\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-48c3e5c70843e13b1e6957f2601ceb0b_l3.png)
![Rendered by QuickLaTeX.com \[u_{\rm{Schw}}^\mu=\left(\Schw^{-1/2},0,0,0\right)\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-c4a86d1b00b5ddd39fca03808b1d8751_l3.png)
![Rendered by QuickLaTeX.com \[\gamma=e\Schw^{-1/2}\qquad V=-\frac{1}{e}\sqrt{e^2-1+\frac{2M}{r}}\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-a90b1978322ac54ce4c637445bc77fed_l3.png)
![Rendered by QuickLaTeX.com \[{u^\mu=\left(e\Schw^{-1},\pm\eroot,0,0\right)\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-18f14260dbcfd3c0686a273a72319a5c_l3.png)
![Rendered by QuickLaTeX.com \[\Schwmetric\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-c9af12fa8aa92d2f1d3a9a32b73b81fc_l3.png)