Month: March 2025

Connection forms and covariant derivatives

In the previous article I introduced Cartan’s connection 1-forms. It is interesting to express various covariant derivatives in terms of them. But firstly:

    \[ \boldsymbol\omega_\mu^{\hphantom\mu\nu} = \omega_{\mu\hphantom\nu\tau}^{\hphantom\mu\nu}\mathbf e^\tau, \qquad\qquad \boldsymbol\omega^\nu_{\hphantom\nu\mu} = \omega^\nu_{\hphantom\nu\mu\tau}\mathbf e^\tau, \]

simply from the definition of covector components. But to check anyway, contract both sides of either equality with \mathbf e_\sigma, to recover the defining formulae. It follows:

    \[ \nabla_\sigma\mathbf e_\mu = \langle\nabla_\sigma\mathbf e_\mu,\mathbf e^\tau\rangle\,\mathbf e_\tau = \omega_{\mu\hphantom\tau\sigma}^{\hphantom\mu\tau}\mathbf e_\tau. \]

To check: the first equality is just components of the vector `\nabla_\sigma\mathbf e_\mu‘. But can check it holds by contracting both sides with \mathbf e^\nu. Similarly for the covector gradients,

    \[ \nabla_\sigma\mathbf e^\nu = \langle\nabla_\sigma\mathbf e^\nu,\mathbf e_\tau\rangle\,\mathbf e^\tau = \omega^\nu_{\hphantom\nu\tau\sigma}\mathbf e^\tau = -\omega_{\tau\hphantom\nu\sigma}^{\hphantom\tau\nu}\mathbf e^\tau. \]

Now, \nabla = \mathbf e^\sigma\otimes\nabla_\sigma. Because: substitute \mathbf X into the left slot (in our convention) of both sides. The RHS becomes: \langle\mathbf e^\sigma,\mathbf X\rangle\nabla_\sigma = X^\sigma\nabla_\sigma = \nabla_{\mathbf X}, by linearity of this slot. Now, apply this identity to \mathbf e_\mu:

    \[ \nabla\mathbf e_\mu = \mathbf e^\sigma\otimes\nabla_\sigma\mathbf e_\mu = \omega_{\mu\hphantom\tau\sigma}^{\hphantom\mu\tau}\mathbf e^\sigma\otimes\mathbf e_\tau = \boldsymbol\omega_\mu^{\hphantom\mu\tau}\otimes\mathbf e_\tau. \]

And:

    \[\begin{split} \nabla\mathbf e^\nu &= e^\sigma\otimes\nabla_\sigma\mathbf e^\nu = \omega^\nu_{\hphantom\nu\tau\sigma}\mathbf e^\sigma\otimes\mathbf e^\tau = -\omega_{\tau\hphantom\nu\sigma}^{\hphantom\tau\nu}\mathbf e^\sigma\otimes\mathbf e^\tau \\ &= \boldsymbol\omega^\nu_{\hphantom\nu\tau}\otimes\mathbf e^\tau = -\boldsymbol\omega_\tau^{\hphantom\tau\nu}\otimes\mathbf e^\tau. \end{split}\]

The antisymmetric part of the covariant derivative is (one half times) the exterior derivative:

    \[\begin{split} d(\mathbf e^\nu) &= \boldsymbol\omega^\nu_{\hphantom\nu\sigma}\wedge\mathbf e^\sigma = \omega^\nu_{\hphantom\nu\sigma\tau}\mathbf e^\tau\wedge\mathbf e^\sigma = -\omega^\nu_{\hphantom\nu\sigma\tau}\mathbf e^\sigma\wedge\mathbf e^\tau \\ &= \omega_{\sigma\hphantom\nu\tau}^{\hphantom\sigma\nu}\mathbf e^\sigma\wedge\mathbf e^\tau. \end{split}\]

This is Cartan’s first structural equation! We have assumed a connection with no torsion.

Cartan’s connection 1-forms

Difficulty:   ★★★★☆   undergraduate / graduate

The connection 1-forms \boldsymbol\omega{_\mu^{\hphantom\mu\nu}} are one way to express a connection \nabla on a manifold. The connection coefficients \Gamma_{\sigma\mu}^{\hphantom{\sigma\mu}\nu} are more familiar and achieve the same purpose, but package the information differently. Connection forms are part of Cartan’s efficient and elegant “moving frames” approach to derivatives and curvature.

[I am only just learning this material, so this article is for my own notes, consolidation of understanding, and checking of conventions. It is a work in progress. There is limited actual derivation in what follows, so don’t be intimidated by the formulae, as they really just introduce notation and a couple of basic properties.]

Write \mathbf e_\mu for a vector basis at each point, and \mathbf e^\nu for its dual basis. For now, we do not assume these frames are orthonormal (in fact, we don’t even need a metric, for now). The connection forms for this basis are: \boldsymbol\omega_\mu^{\hphantom\mu\nu}(\mathbf X) := \langle\nabla_{\mathbf X}\mathbf e_\mu,\mathbf e^\nu\rangle, where \mathbf X is any input vector. (I will sometimes write \langle\cdot,\cdot\rangle for the contraction between a vector and covector, which is not uncommon in the literature. The unified notation with the metric scalar product is convenient, although it is sometimes worth reminding oneself that no metric is needed in this particular case.) To find the components, substitute basis vectors \mathbf X \rightarrow \mathbf e_\sigma:

    \[ \omega_{\mu\hphantom\nu\sigma}^{\hphantom\mu\nu} := \boldsymbol\omega_\mu^{\hphantom\mu\nu}(\mathbf e_\sigma) = \langle\nabla_\sigma\mathbf e_\mu,\mathbf e^\nu\rangle =: \Gamma_{\sigma\mu}^{\hphantom{\sigma\mu}\nu}, \]

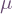where \nabla_\sigma := \nabla_{\mathbf e_\sigma} as usual. Hence with our conventions, the \mu-index specifies which basis vector field is being differentiated, \sigma specifies the direction it is being differentiated in, and \nu specifies the component of the resulting vector. (Lee 2018  Problem 4-14 uses the same convention. MTW  §14.5, Frankel 2012  §9.3b, and Tu 2017  §11.1 would write \boldsymbol\omega^\nu_{\hphantom\nu\mu} for our expression — which swaps the index order.)

We could define separate connection 1-forms \boldsymbol\omega^\nu_{\hphantom\nu\mu} for the dual basis. Note the different index placement. These are:

    \[ \omega\indices^\nu_{\hphantom\nu\mu\sigma} := \boldsymbol\omega^\nu_{\hphantom\nu\mu}(\mathbf e_\sigma) := \langle\nabla_\sigma\mathbf e^\nu,\mathbf e_\mu\rangle = -\langle\nabla_\sigma\mathbf e_\mu,\mathbf e^\nu\rangle = -\omega_{\mu\hphantom\nu\sigma}^{\hphantom\mu\nu}. \]

Hence the two sets of connection forms are related:

    \[ \boldsymbol\omega_\mu^{\hphantom\mu\nu} = -\boldsymbol\omega^\nu_{\hphantom\nu\mu}. \]

Caution: This is not the skew-symmetric relation for an orthonormal basis, which is much more common I think. Here we have not even used a metric, so far. The above uses only the natural duality between vectors and covectors. And it compares two different types of connection forms. The equation used:

    \[ 0 = \nabla_\sigma\langle\mathbf e_\mu,\mathbf e^\nu\rangle = \langle\nabla_\sigma\mathbf e_\mu,\mathbf e^\nu\rangle + \langle\mathbf e_\mu,\nabla_\sigma\mathbf e^\nu\rangle. \]

For the first equality, \langle\mathbf e_\mu,\mathbf e^\nu\rangle = \delta_\mu^{\hphantom\mu\nu} is constant, so its gradient vanishes. The second equality follows from the defining properties of the covariant derivative, i.e. the extension of the connection to covectors and other tensors (e.g. Lee 2018  Prop. 4.15).

[Regarding index placement, and their raising and lowering, I was formerly confused by this issue in the context of vector bases, for a previous blog article. Specifically, to express an arbitrary frame in terms of a coordinate basis, some references write the components as \mathbf e_a^{\hphantom a\mu}. The Latin index is raised and lowered using the metric components in the arbitrary frame, whereas the Greek index uses the metric components in the coordinate frame. However textbooks were not clear on what was definition vs. what was derived, I thought. I eventually concluded the various indices and their placements are best treated as a definition of components, with any formulae for swapping/raising/lowering being obtained from that.]

But let’s now suppose there is a metric, with compatible connection, and an orthonormal basis. Then a common result is: \boldsymbol\omega_\mu^{\hphantom\mu\nu} = -\boldsymbol\omega_\nu^{\hphantom\nu\mu}, in terms of our notation. I did not see how to prove this, so initially I just copied and affirmed it. But I am now updating this 6 months later, and I realise it is only true for a metric of Riemannian signature. Sorry about that.

Instead, considering the gradient of 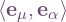\langle\mathbf e_\mu,\mathbf e_\alpha\rangle leads to 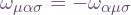\omega_{\mu\alpha\sigma} = -\omega_{\alpha\mu\sigma}. Multiply both sides by 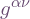g^{\alpha\nu} and sum, which gives:
\omega_{\mu\hphantom\nu\sigma}^{\hphantom\mu\nu} = -\omega_{\alpha\mu\sigma}g^{\alpha\nu}. On the LHS, this raised the second index, which is tensorial or “linear”. But on the RHS, the first index doesn’t obey the tensorial rule. (See the next article I would write on raising and lowering here.) The RHS is equal to: -\omega_{\alpha\hphantom\tau\sigma}^{\hphantom\alpha\tau}g^{\alpha\nu}g_{\tau\mu}. 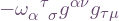Now apply orthonormality again, so the sum collapses to 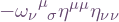-\omega_{\nu\hphantom\mu\sigma}^{\hphantom\nu\mu}\eta^{\mu\mu}\eta_{\nu\nu}, hence:

    \[ \boldsymbol\omega_\mu^{\hphantom\mu\nu} = -\eta_{\mu\mu}\eta_{\nu\nu}\,\boldsymbol\omega_\nu^{\hphantom\nu\mu}. \]

This generalises the orthonormal basis case to Lorentzian signature. Similarly for our alternate connection forms: 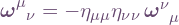\boldsymbol\omega^\mu_{\hphantom\mu\nu} = -\eta_{\mu\mu}\eta_{\nu\nu}\,\boldsymbol\omega^\nu_{\hphantom\nu\mu}.

It is interesting to relate the connection forms to various covariant derivative expressions, but I’ll spin that off into a separate article. I also recently learned (or clarified) that a metric connection may be interpreted as rotations of a frame, a beautiful geometric insight.