Month: September 2025

Difficulty:   ★★★☆☆   undergraduate

[This very rough outline is just a placeholder. I have been putting off writing this article, until I can draw a good diagram.]

“Recall” a connection instructs how to compare vectors at nearby points on a manifold. It is essential for defining what “parallel” means, and taking certain derivatives. In physics, it is typically obtained from a metric. This case is called a metric connection or Levi-Civita connection. The most familiar expression of a connection is the connection coefficients , which are called Christoffel symbols in the special case of a metric connection.

One intuition is the gradient of basis vector (fields). . This decomposes the gradient of one basis vector field in terms of all the basis vectors. In fact, this gradient is expressed in totality by the total covariant derivative … For each fixed value of (and choice of basis), this is actually a tensor, of rank 2.

However an even better one is a map from vectors to rotations. Input vector is the direction a frame is moved along the manifold. (To be slightly more precise, for an “infinitesimal” distance. Though one could certainly be much clearer still.) The output is the rotation the frame undergoes. Relative to the frame (field) already defined there, that is.

Cartan knew this interpretation. For example his book Riemannian geometry in an orthogonal frame is clear. It is not incidental, but infused throughout. Starting with section 1 of chapter 1! I am thoroughly impressed.(While I was well aware Cartan is a famous geometer, naturally I have not read much of his work carefully in the original sources. firsthand, experiential.)

I am deeply passionate about geometric intuition, because I like deep conceptual understanding. Conversely I feel very unsatisfied when equations are presented without meaning behind them — especially things like connections or curvature tensors, in a pedagogical setting. (It must be hard to teach a course on general relativity, where even the requisite differential geometry must be crammed in first. Besides it may not even be a lecturer’s specialty. Hence I am not criticising courses… much. But even most textbooks don’t present the degree of intuition which I would prefer. But at least one piece of good news for me personally is that this gives me an avenue where I can contribute. And I feel enthusiastic about that. Now this won’t actually be original understanding, in many cases. It would be more about drawing attention to under-represented insights.)

It seems intuition sometimes gets lost, historically. One cause seems to be abstraction and generalisation. Now, I have absolutely no problem with those. It is valuable and insightful, and it is good that specialists work on that. But I like to also see clear motivation for introducing a quantity. And knowing the original historical motives by the discoverer(s) can make it more relatable. Covectors are a good example. Even if a strange circuitous route (like a recent video about optics and Lagrangians iirc), because connects to existing insights. Also could add confidence: “I could do that too!” [The opposite is refining and polishing results. Now that is certainly valuable, in fact it is absolutely essential (pragmatically speaking) because it is too much work to read original sources, in most cases. But this already receives tremendous emphasis.]

Difficulty:   ★★☆☆☆   no equations, but some deep concepts

When you first learn some physics of gravity, it is introduced as a force. This is the usual phrasing for Newton’s theory of gravity, whose equations were published in 1687.

But if you then study general relativity (GR) — Einstein’s theory of gravity from 1915 — many textbooks correct you that gravity is not a force, but curvature of spacetime. Congratulations, you have now attained the sophisticated understanding. You have arrived!

…Or have you? When Newtonian gravity is formulated in modern geometric language, it is also interpreted as curvature of space–time. (This uses a manifold with metric(s) and connection, called Newton-Cartan theory.) Hence, the distinction between force and curvature is not about Newton vs Einstein, nor classical vs relativistic, but more about “geometric” formulations vs others.

To throw another spanner in the works, there is a niche approach named teleparallel gravity. Here, gravity is torsion, and there is no curvature at all! The theory uses a different mathematical description than GR, but ends up with the same physical predictions. [Anecdotes: I realised (or re-realised) this interpretation possibility during a lecture at a gravitational waves school at the Physikzentrum in Bad Honnef, Germany in 2019, I think. After the lecture, a Portuguese PhD student and I confirmed with one another what we had heard, and the above consequence. Also in an earlier year, I sat on a streetside kerb in Europe while a young guy (Martin Krššák?) talked passionately to me about teleparallel gravity. We were waiting for some aspect of a conference program to start, perhaps a tour or dinner.]

Yet another concept is inertia. Here I mean a gauge or convention about a “background” velocity or acceleration, for some chosen system at hand. (I am not talking about the more common usage, where inertial motion means geodesic. Regarding another issue, I do not promote an absolute background velocity, as in the aether.) For example, are you sitting still right now, moving at ≈1000 km/h due to Earth’s rotation, or moving at ≈600km/s as determined by the cosmic microwave background? One may ask related questions about acceleration (again, in the sense of an inertial background gauge, not the 4-acceleration from the connection in the usual sense). I will write more on this in the future.

The modern view is that gravitation is curvature alone, since only that is physically measurable, locally. (In a ship floating in space, with no windows so you can’t compare yourself to the distant stars, then uniform inertial motion is not detectable, even in principle.) However I have been rethinking the sufficiency of curvature lately. In Newtonian theory, you can add a constant to the gravitational potential, which has no effect on physical predictions. You can also add a term which effects a background/inertial acceleration; this is constant over space but may vary over time. (Malament 2012  §4.2 has plenty of detail.) I speculate similar gauge choices would apply to relativistic spacetimes too, with appropriate generalisation. I further speculate this is essential for defining gravitational energy, at least in a physical and general way. Another inspiration for going beyond curvature is the Equivalence Principle, a concept which has morphed and diverged quite significantly over the past century. 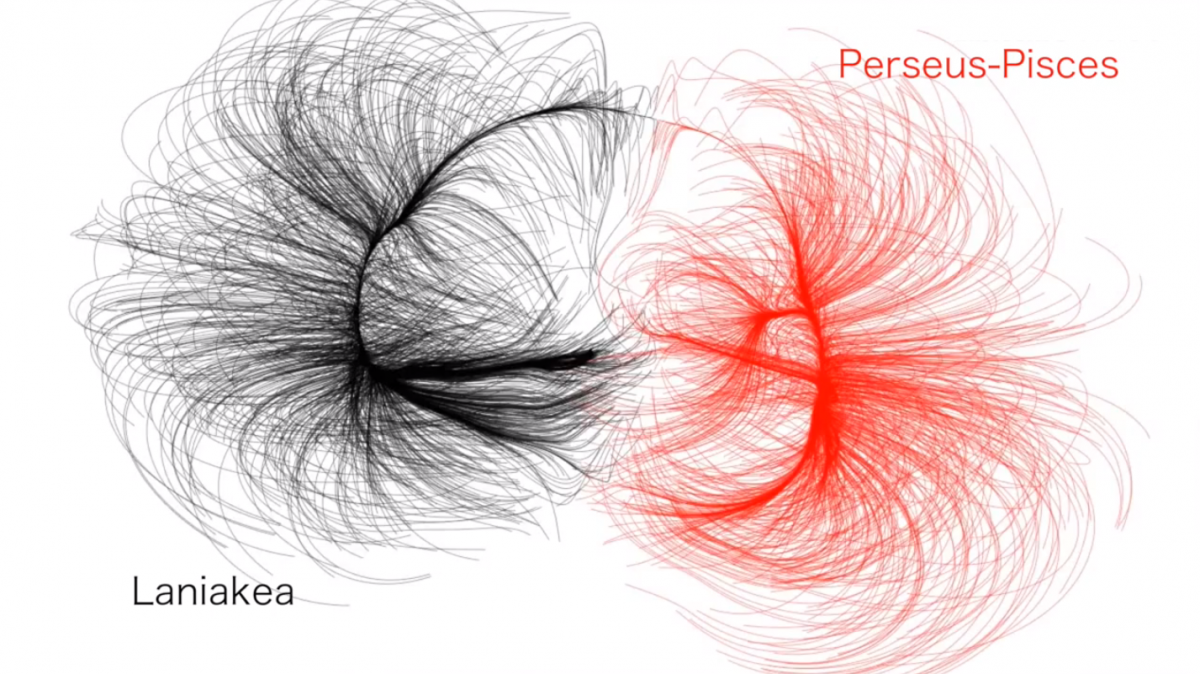But Einstein’s version of it stressed the role of inertia, as Norton (1985)  evaluates in detail. I certainly appreciate the modern curvature-only view for what it affirms, just not what it denies.

In conclusion, there is a curious variety of terminology for gravity: force / curvature / torsion / inertia. Personally I continue to conflate “gravity” with “curvature” in communication, but this is mostly just a reflection of standard usage. In particular I do not imply a rejection of the torsion perspective of teleparallel gravity, but merely my unfamiliarity with it. I also wonder if the “force” interpretation might remain useful when frames are specified, including when gravity is described in a similar way to electromagnetism (called gravitomagnetism). As I understand the usage, we say “force” to suggest deviation from the natural trajectory, so the question becomes, which trajectories will one consider natural? Finally, I tentatively suggest an inertial gauge should be absorbed into the concept of “gravity”, in addition to curvature. However, to compromise with the usual terminology, where gravity means curvature, I’ll settle for the hybrid term “inertia–gravity” instead.

Difficulty:   ★★☆☆☆   high school

The following video shows the paths taken by galaxies and larger structures, within our region of the universe. This cosmic “bulk flow” is based on a huge amount of astrophysical data, analysed in Tully+ 2014 . These researchers dubbed this supercluster of galaxies Laniakea, which is Hawaiian for “open skies” or “immense heaven”. It is about 500 million light-years across, which is 5000 times the length of our Milky Way galaxy! The incredible image in the still frame below stuck in my mind since I watched the video years ago. Its (human) artist is credited here.

The red dot shows the location of the Milky Way. Now, matter in the universe is distributed fairly evenly (it is “homogeneous” and “isotropic”) on very large scales. However gravity causes it to clump together on smaller scales, into stars, galaxies, clusters of galaxies, and so on. A ball-like shape tends to collapse along a single one of its axes first into a sheet or “pancake”, then along another axis into a line or thread-like “filament”, and finally into a more compact blob, as shown theoretically by Zeldovich . In our universe, matter forms a “cosmic web”, which includes filaments with a heavy “node” at the end — a cluster or supercluster. On the other hand, cosmic “voids” are vast regions containing less matter than average. Over time, the matter clumps further, while the voids grow larger and sparser.

The universe is also expanding (which means nothing more than matter moving apart, arguably). For everything discussed here, this expansion has already been subtracted off, so only the “peculiar velocity” remains. In fact Laniakea as a whole is not gravitationally bound. In the distant future it will split into smaller clusters, which will separate as the universe expands. (At least, based on the current understanding of dark energy.) By the way there is no universal agreement on the name Laniakea, nor on its precise boundary.

I remembered this research because I have been wondering about cosmic filaments. (I hoped they might provide a real-world basis for a certain idealised gravitational scenario I have in mind, for some theoretical work. But even if they don’t fulfil this, it is no loss to experience wonder at the beauty in the universe.)

While filaments are vast, they are mostly empty space, hence their gravity is “weak” so Newtonian theory works well. If you model one as cylindrically symmetric, then most of the gravitational force they exert is sideways, onto the filament. However they tend to end in a heavy cluster or supercluster, hence even a galaxy inside the filament will get pulled along its length. The gravitational acceleration of our galaxy and its neighbours (the Local Group) is only about 10^-12m/s² apparently, which is 10 trillion times less than Earth’s surface gravity! However the effect is cumulative, so over vast time scales this is consistent with the ≈600 km/s speed of the Local Group today.