Given a connection  on a manifold, along with any vector basis
on a manifold, along with any vector basis  , the connection coefficients are:
, the connection coefficients are:
![Rendered by QuickLaTeX.com \[ \Gamma_{\mu\nu}^{\hphantom{\mu\nu}\sigma} := \langle\nabla_\mu\mathbf e_\nu,\mathbf e^\sigma\rangle. \]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-0da3696c8ef5490c24c4ced6dac4df8f_l3.png)
[For the usual connection based on a metric, these are called Christoffel symbols. On rare occasions some add “…of the second kind”, which we will interpret to mean the component of the output is the only raised index. Also the coefficients may be packaged into Cartan’s connection 1-forms, with components  , as introduced in the previous article. Hence raising or lowering indices on the connection forms is the same problem.]
, as introduced in the previous article. Hence raising or lowering indices on the connection forms is the same problem.]
In our convention, the first index specifies the direction  of differentiation, the second is the basis vector (field) being differentiated, and the last index is for the component of the resulting vector. We use the same angle bracket notation for the metric scalar product, inverse metric scalar product, and the contraction of a vector and covector (as above; and this does not require a metric).
of differentiation, the second is the basis vector (field) being differentiated, and the last index is for the component of the resulting vector. We use the same angle bracket notation for the metric scalar product, inverse metric scalar product, and the contraction of a vector and covector (as above; and this does not require a metric).
This unified notation is very convenient for generalising the above connection coefficients to any variant of raised or lowered indices, as we will demonstrate by examples. We will take such variants on the original equation as a definition, then the relation to the original  variant will be derived from that.
variant will be derived from that.
[Regarding index placement and their raising and lowering, I was formerly confused by this issue, in the case of non-tensorial objects, or using different vector bases for different indices. For example, to express an arbitrary frame in terms of a coordinate basis, some references write the components as 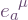 , as blogged previously. The Latin index is raised and lowered using the metric components in the general frame
, as blogged previously. The Latin index is raised and lowered using the metric components in the general frame  , whereas for the Greek index the metric components in a coordinate frame
, whereas for the Greek index the metric components in a coordinate frame 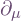 are used. However while these textbook(s) gave useful practical formulae, I did not find them clear on what was definition vs. what was derived. I eventually concluded the various indices and their placements are best treated as a definition of components, with any formulae for swapping / raising / lowering being obtained from that.]
are used. However while these textbook(s) gave useful practical formulae, I did not find them clear on what was definition vs. what was derived. I eventually concluded the various indices and their placements are best treated as a definition of components, with any formulae for swapping / raising / lowering being obtained from that.]
The last index is the most straightforward. We define:  , with all indices lowered. These quantities are the overlaps between the vectors
, with all indices lowered. These quantities are the overlaps between the vectors  and
and  . [Incidentally we could call them the “components” of
. [Incidentally we could call them the “components” of  , if this vector is decomposed in the alternate vector basis
, if this vector is decomposed in the alternate vector basis  . After all, for any vector,
. After all, for any vector,  , which may be checked by contracting both sides with
, which may be checked by contracting both sides with  . ] To relate to the original
. ] To relate to the original  s, note:
s, note:
![Rendered by QuickLaTeX.com \[ \Gamma_{\mu\nu\tau} = \langle\nabla_\mu\mathbf e_\nu,\mathbf e^\sigma g_{\sigma\tau}\rangle = \langle\nabla_\mu\mathbf e_\nu,\mathbf e^\sigma\rangle g_{\sigma\tau} = \Gamma_{\mu\nu}^{\hphantom{\mu\nu}\sigma}g_{\sigma\tau}, \]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-1e8dc7263a128cfd70916ce655732f69_l3.png)
using linearity. Hence this index is raised or lowered using the metric, as familiar for an index of a tensor. We could say it is a “tensorial” index. The output  of the derivative is just a vector, after all. The
of the derivative is just a vector, after all. The  have been called “Christoffel symbols of the first kind”.
have been called “Christoffel symbols of the first kind”.
The first index is also fairly straightforward. We define a raised version by:  . However, this begs the question of what the notation ‘
. However, this begs the question of what the notation ‘ ’ means. The raised index suggests
’ means. The raised index suggests  , which is a covector, but we can take its dual using the metric (assuming there is one). Hence
, which is a covector, but we can take its dual using the metric (assuming there is one). Hence  is a sensible definition, or for an arbitrary covector,
is a sensible definition, or for an arbitrary covector,  . (For those not familiar with the notation,
. (For those not familiar with the notation,  is simply the vector with components
is simply the vector with components  .)
.)
These duals are related to the vectors of the original basis by:  , where
, where  are still the inverse metric components for the original basis. Hence
are still the inverse metric components for the original basis. Hence  , by the linearity of this slot. In terms of the coefficients,
, by the linearity of this slot. In terms of the coefficients,  , hence the first index is also “tensorial”.
, hence the first index is also “tensorial”.
Finally, the middle index has the most interesting properties for raising or lowering. Let’s start with a raised middle index and lowered last index:  . This means it is now a covector field which is being differentiated, and the components of the result are peeled off. For their relation to the original coefficients, note firstly
. This means it is now a covector field which is being differentiated, and the components of the result are peeled off. For their relation to the original coefficients, note firstly  , since these bases are dual. These are constants, hence their gradients vanish:
, since these bases are dual. These are constants, hence their gradients vanish:
![Rendered by QuickLaTeX.com \[ 0 = \nabla_\mu \langle\mathbf e^\sigma,\mathbf e_\nu\rangle = \langle\nabla_\mu\mathbf e^\sigma,\mathbf e_\nu\rangle + \langle\mathbf e^\sigma,\nabla_\mu\mathbf e_\nu\rangle. \]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-0f37b17e9f5fc89208a9b894a85bb478_l3.png)
[The second equality is not the metric-compatibility property of some connections, despite looking extremely similar in our notation. No metric is used here. Rather, it is a defining property of the covariant derivative; see e.g. Lee 2018  Prop. 4.15. But no doubt these defining properties are chosen for their “compatibility” with the vector–covector relationship.]
Prop. 4.15. But no doubt these defining properties are chosen for their “compatibility” with the vector–covector relationship.]
Hence  . Note the order of the last two indices is swapped in this expression, and their “heights” are also changed. (I mean, it is not just that
. Note the order of the last two indices is swapped in this expression, and their “heights” are also changed. (I mean, it is not just that  and
and  are interchanged.) This relation is antisymmetric in some sense, and looks more striking in notation which suppresses the first index. Connection 1-forms (can) do exactly that:
are interchanged.) This relation is antisymmetric in some sense, and looks more striking in notation which suppresses the first index. Connection 1-forms (can) do exactly that:  .
.
Note this is not the well-known property for an orthonormal basis, which is  using our conventions. Both equalities follow from conveniently chosen properties of bases: the dual basis relation in the former case, and orthonormality of a single basis in the latter. Our relation holds in any basis, and does not require a metric. But both relations are useful — they just apply to different contexts.
using our conventions. Both equalities follow from conveniently chosen properties of bases: the dual basis relation in the former case, and orthonormality of a single basis in the latter. Our relation holds in any basis, and does not require a metric. But both relations are useful — they just apply to different contexts.
To isolate the middle index as the only one changed, raise the last index again:  . Only now have we invoked the metric, in our discussion of the middle index.
. Only now have we invoked the metric, in our discussion of the middle index.
The formula  has an elegant simplicity. However at first it didn’t feel right to me as the sought-after relation. We are accustomed to tensors, where a single index is raised or lowered independently of the others. However in this case the middle index describes a vector which is differentiated, and differentiation is not linear (for our purposes here), but obeys a Leibniz rule. (To be precise, it is linear over sums, and multiplication by a constant scalar. It is not linear under multiplication by an arbitrary scalar. Mathematicians call this
has an elegant simplicity. However at first it didn’t feel right to me as the sought-after relation. We are accustomed to tensors, where a single index is raised or lowered independently of the others. However in this case the middle index describes a vector which is differentiated, and differentiation is not linear (for our purposes here), but obeys a Leibniz rule. (To be precise, it is linear over sums, and multiplication by a constant scalar. It is not linear under multiplication by an arbitrary scalar. Mathematicians call this  -linear but not
-linear but not  -linear.)
-linear.)
The formula could be much worse. Suppose we replaced the original equation with an arbitrary operator, and defined raised and lowered coefficients similarly. Assuming the different variants are related somehow, then in general each could depend on all coefficients from the original variant, for example:  , for some functions
, for some functions 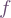 with 3 × 2 = 6 indices.
with 3 × 2 = 6 indices.
Much of the material here is not uncommon. In differential geometry it is well-known the connection coefficients are not tensors. And it is not rare to hear that in fact two of their indices do behave tensorially. But I do not remember seeing a clear definition of what it means to raise or lower any index, in the literature. (Though the approach in geometric algebra, of using two distinct vector bases  and
and  , is similar. This requires a metric, and gives a unique interpretation to raising and lowering indices. But in fairness, most transformations we have described also require a metric.) Most textbooks probably do not define different variants of the connection forms, although I have not investigated this much at present.
, is similar. This requires a metric, and gives a unique interpretation to raising and lowering indices. But in fairness, most transformations we have described also require a metric.) Most textbooks probably do not define different variants of the connection forms, although I have not investigated this much at present.
Finally, it is easy to look back and say something is straightforward. But not when your attention is preoccupied with grasping the core aspects of a new thing, not its more peripheral details. When I was first learning about connection forms, it was not at all clear whether you could raise or lower their indices. Because the few references I consulted didn’t mention this at all, to me it felt like it should be obvious. But it is not obvious, and demands careful consideration, even though some results are familiar ideas in a new context.
![]() instructs how to compare vectors at nearby points on a manifold. It is essential for defining what “parallel” means, and taking certain derivatives. In physics, it is typically obtained from a metric. This case is called a metric connection or Levi-Civita connection. The most familiar expression of a connection is the connection coefficients
instructs how to compare vectors at nearby points on a manifold. It is essential for defining what “parallel” means, and taking certain derivatives. In physics, it is typically obtained from a metric. This case is called a metric connection or Levi-Civita connection. The most familiar expression of a connection is the connection coefficients ![]() , which are called Christoffel symbols in the special case of a metric connection.
, which are called Christoffel symbols in the special case of a metric connection.![]() . This decomposes the gradient of one basis vector field in terms of all the basis vectors. In fact, this gradient is expressed in totality by the total covariant derivative
. This decomposes the gradient of one basis vector field in terms of all the basis vectors. In fact, this gradient is expressed in totality by the total covariant derivative ![]() … For each fixed value of
… For each fixed value of ![]() (and choice of basis), this is actually a tensor, of rank 2.
(and choice of basis), this is actually a tensor, of rank 2. is clear. It is not incidental, but infused throughout. Starting with section 1 of chapter 1! I am thoroughly impressed.(While I was well aware Cartan is a famous geometer, naturally I have not read much of his work carefully in the original sources. firsthand, experiential.)
is clear. It is not incidental, but infused throughout. Starting with section 1 of chapter 1! I am thoroughly impressed.(While I was well aware Cartan is a famous geometer, naturally I have not read much of his work carefully in the original sources. firsthand, experiential.) evaluates in detail. I certainly appreciate the modern curvature-only view for what it affirms, just not what it denies.
evaluates in detail. I certainly appreciate the modern curvature-only view for what it affirms, just not what it denies. . In our universe, matter forms a “cosmic web”, which includes filaments with a heavy “node” at the end — a cluster or supercluster. On the other hand, cosmic “voids” are vast regions containing less matter than average. Over time, the matter clumps further, while the voids grow larger and sparser.
. In our universe, matter forms a “cosmic web”, which includes filaments with a heavy “node” at the end — a cluster or supercluster. On the other hand, cosmic “voids” are vast regions containing less matter than average. Over time, the matter clumps further, while the voids grow larger and sparser.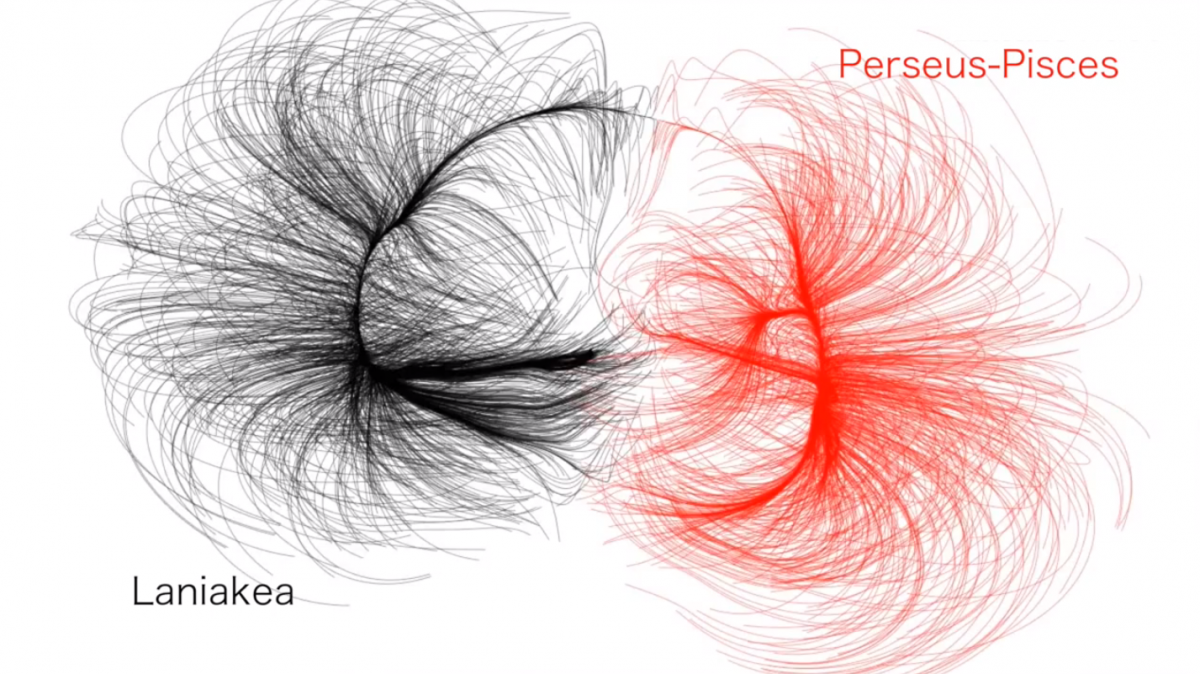
 \mathfrak{su}(3)
\mathfrak{su}(3) \epsilon
\epsilon![Rendered by QuickLaTeX.com \[\begin{split} \nabla\mathbf e^\nu &= e^\sigma\otimes\nabla_\sigma\mathbf e^\nu = \omega^\nu_{\hphantom\nu\tau\sigma}\mathbf e^\sigma\otimes\mathbf e^\tau = -\omega_{\tau\hphantom\nu\sigma}^{\hphantom\tau\nu}\mathbf e^\sigma\otimes\mathbf e^\tau \\ &= \boldsymbol\omega^\nu_{\hphantom\nu\tau}\otimes\mathbf e^\tau = -\boldsymbol\omega_\tau^{\hphantom\tau\nu}\otimes\mathbf e^\tau. \end{split}\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-9faf56c751b9f2cc0c5b5ad6fee9bd9e_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split} d(\mathbf e^\nu) &= \boldsymbol\omega^\nu_{\hphantom\nu\sigma}\wedge\mathbf e^\sigma = \omega^\nu_{\hphantom\nu\sigma\tau}\mathbf e^\tau\wedge\mathbf e^\sigma = -\omega^\nu_{\hphantom\nu\sigma\tau}\mathbf e^\sigma\wedge\mathbf e^\tau \\ &= \omega_{\sigma\hphantom\nu\tau}^{\hphantom\sigma\nu}\mathbf e^\sigma\wedge\mathbf e^\tau. \end{split}\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-b93a68da7af62887c0b6ec1cf1a7a72c_l3.png)

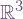 . In the diagram we index the vectors by colour, rather than the typical 1, 2, and 3. Rather than using a co-basis of covectors as in the standard modern approach, we take both bases to be made up of vectors. Note for example, the red vector on the right is orthogonal to the blue and green vectors on the left. (I made up the directions when plotting, so don’t expect everything to be quantifiably correct.) Arguably “inverse basis” would be the best name. Finally I would prefer to start from this picture, as it is simple and intuitive, rather than start with covectors and musical isomorphisms. Maybe next time I will be brave enough.
. In the diagram we index the vectors by colour, rather than the typical 1, 2, and 3. Rather than using a co-basis of covectors as in the standard modern approach, we take both bases to be made up of vectors. Note for example, the red vector on the right is orthogonal to the blue and green vectors on the left. (I made up the directions when plotting, so don’t expect everything to be quantifiably correct.) Arguably “inverse basis” would be the best name. Finally I would prefer to start from this picture, as it is simple and intuitive, rather than start with covectors and musical isomorphisms. Maybe next time I will be brave enough.![Rendered by QuickLaTeX.com \[\begin{tabular}{|c|c|c|}\hline $\frac{p^2+q^2+r^2+s^2}{u}$ & $\frac{2(qr+ps)}{u}$ & $\frac{2(qs-pr)}{u}$ \\ \hline $\frac{2(qr-ps)}{u}$ & $\frac{p^2-q^2+r^2-s^2}{u}$ & $\frac{2(pq+rs)}{u}$ \\ \hline $\frac{2(qs+pr)}{u}$ & $\frac{2(rs-pq)}{u}$ & $\frac{p^2-q^2-r^2+s^2}{u}$ \\ \hline\end{tabular},\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-8a820b1a5889a514cf73584ad468f584_l3.png)

