Month: April 2021

Affine connection for spherical symmetry

Difficulty:   ★★★★☆   graduate

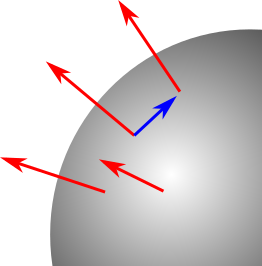
Suppose you have a spherically symmetric vector field, as in the diagram. Can we find an affine connection which transports the vectors into one-another? That is, a geometry in which they are all “parallel”?

Portion of a sphere, with vectors orthogonal to its surface
The vectors (red arrows) are clearly not parallel in the usual sense. But can we define a new connection in which they are transported into one-another?

Take Schwarzschild spacetime, in the usual coordinates (t,r,\theta,\phi). The coordinate basis vectors are \partial_t, \partial_r, \partial_\theta, and \partial_\phi. I will write these as \mathbf e_\mu, so for \mu = 1 for example, this is the vector \mathbf e_r with components (e_r)^\nu = (0,1,0,0). Recall a connection \nabla is defined by:

    \[\nabla_{\mathbf e_\mu}\mathbf e_\nu = \Gamma^\alpha_{\mu\nu}\mathbf e_\alpha,\]

where the \Gamma are the connection coefficients, also called Christoffel symbols in the specific case of the Levi-Civita connection. (Recall the Levi-Civita connection is the one inherited from the metric: it is the unique symmetric and metric-compatible connection.) For each pair (\mu,\nu), this definition is interpreted as the derivative of the \mathbf e_\nu field, in the direction \mathbf e_\mu.

Now consider an arbitrary vector field of the form:

    \[u^\mu = (A(t,r),B(t,r),0,0).\]

We would not expect the sought-for parallel transport to work for vectors with components in the \theta or \phi-directions — at least, not without imposing extra choices. In particular, the “hairy ball theorem” states no smooth, non-vanishing vector field along the 2-sphere exists: that is, within its 2-dimensional tangent bundle. For Schwarzschild spacetime, we move around a 2-sphere of constant t and r, by taking “directional derivatives” along the \theta\phi-plane. As expected, \nabla\mathbf u does not vanish, even in these directions:

    \[\nabla_{C\partial_\theta + D\partial_\phi}\mathbf u = \Big(0,0,\frac{C B(t,r)}{r},\frac{D B(t,r)}{r}\Big).\]

The offending Christoffel symbols turn out to be \Gamma_{\theta r}^\theta = 1/r and \Gamma_{\phi r}^\phi = 1/r. These arise from \nabla_{\partial_\theta}\partial_r = r^{-1}\partial_\theta and \nabla_{\partial_\phi}\partial_r = r^{-1}\partial_\phi. These quantify how the radial coordinate vector changes as you move around on a sphere.

One option is to simply define new connection coefficients for which these vanish: \tilde\Gamma_{\theta r}^\theta := 0 and \tilde\Gamma_{\phi r}^\phi := 0, and keep the remaining Christoffel symbols, in order to remain as close as possible to the metric connection. This procedure is justified, because given a frame field, any choice of smooth functions \tilde\Gamma^\alpha_{\mu\nu} yields a valid connection (Lee 2018 , Introduction to Riemannian manifolds, Lemma 4.10). We can also write this new connection as the usual (Levi-Civita) covariant derivative plus a bilinear correction:

    \[\tilde\nabla_{\mathbf v}\mathbf u := \nabla_{\mathbf v}\mathbf u - \frac{1}{r} \big(\partial_\theta\otimes d\theta\otimes dr + \partial_\phi\otimes d\phi\otimes dr)(\mathbf v,\mathbf u).\]

The parenthetical term is a (1,2)-tensor we interpret as accepting the vectors in the last two slots (\mathbf v in the second slot, and \mathbf u into the last), returning another vector. The correction term may also be written -\frac{1}{r}\langle dr,\mathbf u\rangle \big(\langle d\theta,\mathbf v\rangle\partial_\theta + \langle d\phi,\mathbf v\rangle\partial_\phi\big), where the angle brackets mean contraction of a 1-form and vector in this case. Intuitively, the parenthetical term just above is also a projection, returning only the angular part of the differentiation direction \mathbf v. This is the blue arrow in the original diagram. For large r, the basis vectors \partial_\theta and \partial_\phi grow very large, but the red \mathbf u vectors must adjust only by the angle rotated through, hence the 1/r multiplier. \langle dr,\mathbf u\rangle returns the radial component u^r.

As a check, \tilde\nabla_{C\partial_\theta+D\partial_\phi}\mathbf u = 0 as required. The new connection is not symmetric, because \tilde\Gamma_{r\theta}^\theta and \tilde\Gamma_{r\phi}^\phi remain non-vanishing. Hence the connection has “torsion”. I won’t write out its Riemann and Ricci tensors, but the scalar curvature is 2/r^2! At face value this violates the Einstein field equations, for which the Ricci tensor (and hence the scalar curvature) always vanish in a vacuum, however Einstein’s equations use the Levi-Civita connection. Curiously, the value is precisely the scalar curvature for a 2-sphere.

We can also construct a symmetric connection \bar\nabla for which additionally \bar\Gamma_{r\theta}^\theta := 0 =: \bar\Gamma_{r\phi}^\phi. In the (somewhat) index-free expression:

    \[\bar\nabla_{\mathbf v}\mathbf u := \nabla_{\mathbf v}\mathbf u - \frac{2}{r} \big(\partial_\theta\otimes dr\,d\theta + \partial_\phi\otimes dr\,d\phi)(\mathbf v,\mathbf u),\]

where 2dr\,d\theta := dr\otimes d\theta + d\theta\otimes dr is the symmetric product, and analogously for dr\,d\phi. This connection has Ricci tensor equal to the metric in the t and r components, apart from a scalar factor 2M/r^3, and vanishing elsewhere. Its scalar curvature is 4M/r^3.

Hence we have constructed connections which parallel transport our spherically symmetric vector field around a sphere, and deviate as little as possible from the Levi-Civita connection. Neither of the new connections are “metric-compatible”, for instance 0 = \tilde\nabla_{\partial_\theta}\langle\partial_r,\partial_\theta\rangle \ne \langle\tilde\nabla_{\partial_\theta}\partial_r,\partial_\theta\rangle + \langle\partial_r,\tilde\nabla_{\partial_\theta}\partial_\theta\rangle = -r. Hence \tilde\nabla\mathbf g \ne 0. The same holds for \bar\nabla.

If you find some formulae here do not work for you, compare your convention for the connection coefficient index order, or try swapping \mathbf u and \mathbf v in the correction terms. I had problems myself, so undertook a painstaking review of my own conventions, and wrote a new page describing them. Finally, beware of coordinate basis vectors! The “vectors” \partial_\theta and \partial_\phi actually depend on all four coordinates, which is related to the so-called “second fundamental confusion of calculus”! In case of ambiguity, perhaps some should be replaced with (d\theta)^\sharp and (d\phi)^\sharp, or scalar multiples thereof. I avoided this technicality in the interests of readability. This concern only applies to coordinate systems in which the metric is non-diagonal.