The discovery of spinors is most often credited to quantum physicists in the 1920s, and to Élie Cartan in the prior decade for an abstract mathematical approach. But it turns out the legendary mathematician Leonhard Euler discovered certain algebraic properties for the usual (2-component, Pauli) spinors, back in the 1700s! He gave a parametrisation for rotations in 3D, using essentially what were later known as Cayley-Klein parameters. There was not even the insight that each set of parameter values forms an interesting object in its own right. But we can recognise one key conceptual aspect of spinors in this accidental discovery: the association with rotations.
In 1771, Euler published a paper on orthogonal transformations, whose title translates to: “An algebraic problem that is notable for some quite extraordinary relations”. Euler scholars index it as “E407”, and the Latin original  is available from the Euler Archive website. I found an English translation
is available from the Euler Archive website. I found an English translation  online, which also transcribes the original language.
online, which also transcribes the original language.
Euler commences with the aim to find “nine numbers… arranged… in a square” which satisfy certain conditions. In modern notation this is a matrix M say, satisfying ![]() , which describes an orthogonal matrix. While admittedly the paper is mostly abstract algebra, he is also motivated by geometry. In §3 he mentions that the equation for a surface is “transformed” under a change of [Cartesian] coordinates, including the case where the coordinate origins coincide. We recognise this (today, at least) as a rotation, possibly combined with a reflection. Euler also mentions “angles” (§4 and later), which is clearly geometric language.
, which describes an orthogonal matrix. While admittedly the paper is mostly abstract algebra, he is also motivated by geometry. In §3 he mentions that the equation for a surface is “transformed” under a change of [Cartesian] coordinates, including the case where the coordinate origins coincide. We recognise this (today, at least) as a rotation, possibly combined with a reflection. Euler also mentions “angles” (§4 and later), which is clearly geometric language.
He goes on to analyse orthogonal transformations in various dimensions. [I was impressed with the description of rotations about n(n – 1)/2 planes, in n dimensions, because I only first learned this in the technical context of higher-dimensional rotating black holes. It is only in 3D that rotations are specified by axis vectors.] Then near the end of the paper, Euler seeks orthogonal matrices containing only rational entries, a “Diophantine” problem. Recall rotation matrices typically contain many trigonometric terms like sin(θ) and cos(θ), which are irrational numbers for most values of the parameter θ. But using some free parameters “p, q, r, s”, Euler presents:
![Rendered by QuickLaTeX.com \[\begin{tabular}{|c|c|c|}\hline $\frac{p^2+q^2+r^2+s^2}{u}$ & $\frac{2(qr+ps)}{u}$ & $\frac{2(qs-pr)}{u}$ \\ \hline $\frac{2(qr-ps)}{u}$ & $\frac{p^2-q^2+r^2-s^2}{u}$ & $\frac{2(pq+rs)}{u}$ \\ \hline $\frac{2(qs+pr)}{u}$ & $\frac{2(rs-pq)}{u}$ & $\frac{p^2-q^2-r^2+s^2}{u}$ \\ \hline\end{tabular},\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-8a820b1a5889a514cf73584ad468f584_l3.png)
where ![]() . (I have copied the style which Euler uses in some subsequent examples.) By choosing rational values of the parameters, the matrix entries will also be rational, however this is not our concern here. The matrix has determinant +1, so we know it represents a rotation. It turns out the parameters form the components of a spinor!!
. (I have copied the style which Euler uses in some subsequent examples.) By choosing rational values of the parameters, the matrix entries will also be rational, however this is not our concern here. The matrix has determinant +1, so we know it represents a rotation. It turns out the parameters form the components of a spinor!! ![]() are the real components of a normalised spinor. We allow all real values, but will ignore some trivial cases. One aspect of spinors is clear from inspection: in the matrix the parameters occur only in pairs, hence the sets of values
are the real components of a normalised spinor. We allow all real values, but will ignore some trivial cases. One aspect of spinors is clear from inspection: in the matrix the parameters occur only in pairs, hence the sets of values ![]() and
and ![]() give rise to the same rotation matrix. (Those familiar with spinors will recall the spin group is the “double cover” of the rotation group.)
give rise to the same rotation matrix. (Those familiar with spinors will recall the spin group is the “double cover” of the rotation group.)
The standard approach is to combine the parameters into two complex numbers. But in the geometric algebra (or Clifford algebra) interpretation, a spinor is a rotation of sorts, or we might say a “half-rotation”. It is about the following plane:
![]()
(For those who haven’t seen the wedge product nor bivectors, you can visualise ![]() for example, as the parallelogram or plane spanned by those vectors. It also has a magnitude and handedness/orientation.) The sum is itself a plane, because we are in 3D. Dividing by
for example, as the parallelogram or plane spanned by those vectors. It also has a magnitude and handedness/orientation.) The sum is itself a plane, because we are in 3D. Dividing by ![]() gives a unit bivector. For the spinor, the angle of rotation θ/2 say, is given by (c.f. Doran & Lasenby 2003
gives a unit bivector. For the spinor, the angle of rotation θ/2 say, is given by (c.f. Doran & Lasenby 2003  §2.7.1):
§2.7.1):
![]()
This determines θ/2 to within a range of 2π (if we include also the orientation of the plane). In contrast, the matrix given earlier effects a rotation by θ — twice the angle — about the same plane. This is because geometric algebra formulates rotations using two copies of the spinor. The matrix loses information about the sign of the spinor, and hence also any distinction between one or two full revolutions.
Euler extends the challenge of finding orthogonal matrices with rational entries to 4D. In §34 he parametrises matrices using “eight numbers at will a, b, c, d, p, q, r, s”. However the determinant of this matrix is -1, so it is not a rotation, and the parameters cannot form a spinor. Two of its eigenvalues are -1 and +1. Now the eigenvectors corresponding to distinct eigenvalues are orthogonal (a property most familiar for symmetric matrices, but it holds for orthogonal matrices also). It follows the matrix causes reflection along one axis, fixes an orthogonal axis, and rotates about the remaining plane. So it does not “include every possible solution” (§36). But I guess the parameters might form a subgroup of the Pin(4) group, the double cover of the 4-dimensional orthogonal group O(4).
Euler provides another 4×4 orthogonal matrix satisfying additional properties, in §36. This one has determinant +1, hence represents a rotation. It would appear no eigenvalues are +1 in general, so it may represent an arbitrary rotation. I guess the parameters ![]() , where I label by u the quantity
, where I label by u the quantity ![]() mentioned by Euler, might form spinors of 4D space (not 3+1-dimensional spacetime). If so, these are members of Spin(4), the double cover of the 4D rotation group SO(4).
mentioned by Euler, might form spinors of 4D space (not 3+1-dimensional spacetime). If so, these are members of Spin(4), the double cover of the 4D rotation group SO(4).
Euler was certainly unaware of his implicit discovery of spinors. His motive was to represent rotations using rational numbers, asserting these are “most suitable for use” (§11). Probably more significant today is that rotations are described by rational functions of spinor components. But the fact spinors would be rediscovered repeatedly in different applications suggests there is something very natural or Platonic about them. Euler says his 4D “solution deserves the more attention”, and that with a general procedure for this and higher dimensions, “Algebra… would be seen to grow very much.” (§36) He could not have anticipated how deserving of attention spinors are, nor their importance in algebra and elsewhere!


![Rendered by QuickLaTeX.com \[\begin{aligned}c_{i,n} &:= P(i\textrm{ died on }n|I\textrm{ dies on }N) \\ &= \frac{b_{I-i,N-n}b_{i,n}}{b_{I,N}} \\ &= \frac{\binom{N-n-1}{I-i-1}\binom{n-1}{i-1}}{\binom{N-1}{I-1}}.\end{aligned}\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-0fdbd6c888443c4ffb02f41beb3ab8bb_l3.png)
![Rendered by QuickLaTeX.com \[\begin{aligned}\frac{c_{i-1,n}}{c_{i,n}} &= \frac{(i-1)(N-I-n+i)}{(I-i)(n-i+1)}, \\ \frac{c_{i,n-1}}{c_{i,n}} &= \frac{(N-n)(n-i)}{(n-1)(N-I-n+i+1)}.\end{aligned}\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-23abcecbb3de8058f61c88bc262b341a_l3.png)
![Rendered by QuickLaTeX.com \[c_{i,n} \equiv \frac{i\binom{N-I}{n-i}\binom{I-1}{i}}{n\binom{N-1}{n}}.\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-8c9a9276cb95c0054bd27bee7f5646bd_l3.png)
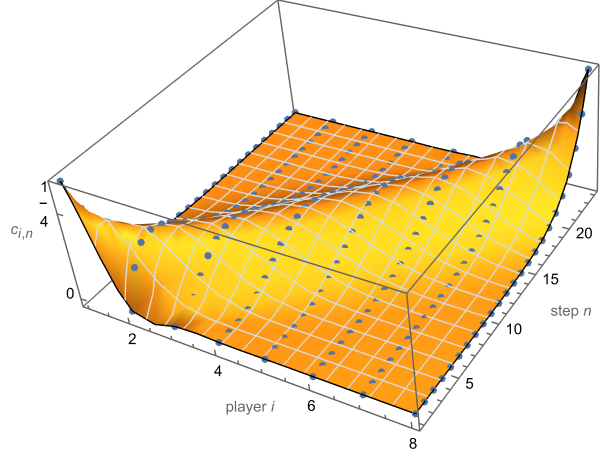
![Rendered by QuickLaTeX.com \[-\frac{\Big(i-\frac{N+nI-I-2n}{N-2}\Big)^2}{(n-1)(N-n-1)/2(N-2)}.\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-243c5e79f2f06bb5cc95404001c8b671_l3.png)
![Rendered by QuickLaTeX.com \[f(x) := \binom{x}{a}\binom{X-x}{b}.\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-1c69da7feadf7542bab4557bbee83d88_l3.png)
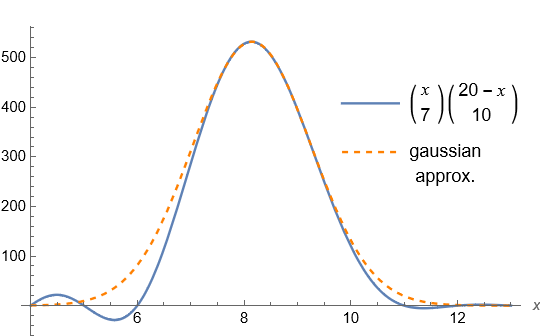
![Rendered by QuickLaTeX.com \[\frac{f(x-1/2)}{f(x+1/2)} = \frac{(x-a+1/2)(X+1/2-x)}{(x+1/2)(X-b+1/2-x)},\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-57dd3410e47df89c49bba1c3de59ad63_l3.png)
![Rendered by QuickLaTeX.com \[x_0 := \frac{2aX+a-b}{2(a+b)}.\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-e1e66503da60cec1c6fbc07436179f21_l3.png)
![Rendered by QuickLaTeX.com \[\frac{2C(a+b)^3}{(2aX+a-b)(2bX-2b^2-2ab+a+3b)},\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-246c69ac64e3e9b91c1b8ecff72861e3_l3.png)
![Rendered by QuickLaTeX.com \[\hat\sigma^2 := \frac{-2C(aX-b)(bX+a+2b)(bX-b^2-ab+a+2b)(aX-a^2-ab-b)}{E(a+b)^6}.\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-26104a688f522ab5ac0d8b4cead8903b_l3.png)
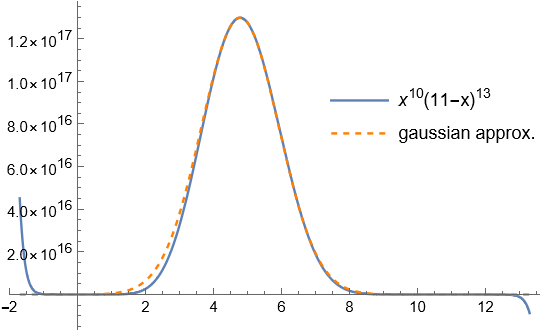
 , and for each non-integer exponent the tail on one side becomes imaginary.
, and for each non-integer exponent the tail on one side becomes imaginary.![Rendered by QuickLaTeX.com \[\tilde x := \frac{X}{1+B/A},\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-63503dd0564d1a52ac96d3a1640448a1_l3.png)
![Rendered by QuickLaTeX.com \[\sigma^2 = \frac{AB}{(A+B)^3}X^2 \equiv \frac{B}{A^2X}\tilde x^3.\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-a9b3e559a77aa85b702f021ab451ce4b_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{(B/A)^B \tilde x^{A+B} \operatorname{exp}\Big( -\frac{(x-\tilde x)^2}{2B\tilde x^3/A^2X} \Big).}\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-231edb19ae54a811f95077fe10c1f232_l3.png)
![Rendered by QuickLaTeX.com \[\int_0^X x^A(X-x)^Bdx = \frac{X^{A+B+1}}{(A+B+1)\binom{A+B}{A}}.\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-62f1b0ae17cb0881a5e0f7f01c59ce05_l3.png)
![Rendered by QuickLaTeX.com \[\int\cdots \approx \frac{\sqrt{2\pi(A+B)}}{A+B+1}(B/A)^{B+1/2}\tilde x^{A+B+1},\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-8e45ac6bded4d3733a9f18fd0fe8b6d3_l3.png)
![Rendered by QuickLaTeX.com \[\int_{-\infty}^\infty \operatorname{exp}\cdots = \sqrt\frac{2\pi}{A+B}(B/A)^{B+1/2}\tilde x^{A+B+1}.\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-6a1d3bd57315c5c72453e2f129c53372_l3.png)
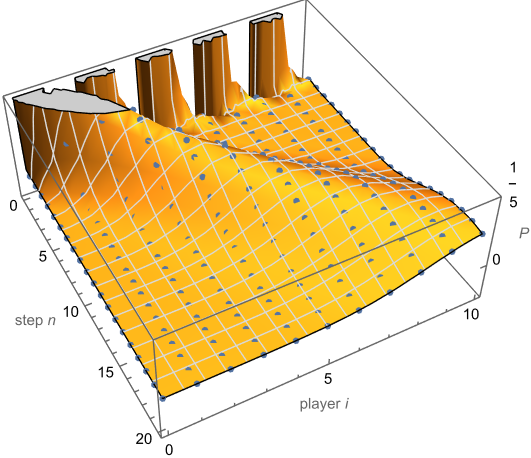
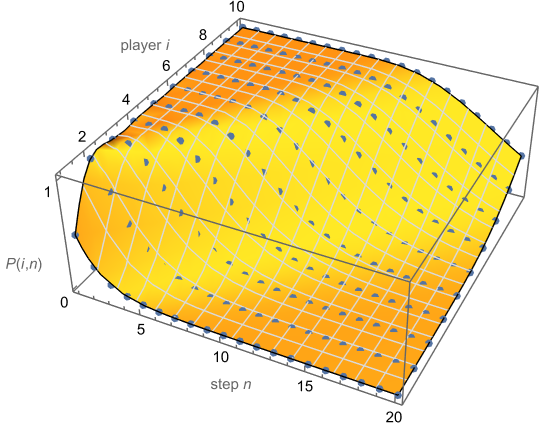
![Rendered by QuickLaTeX.com \[P(i,n) = 1 - \binom{n}{i}\cdot{_2F_1}(i,n+1,i+1;-1),\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-7eed551eaac81352e796d57756cf7150_l3.png)

![Rendered by QuickLaTeX.com \[P(i,2i) = \frac{1}{2} - \frac{\Gamma(i+1/2)}{2\sqrt\pi\,\Gamma(i+1)},\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-ee8acac2cd458ac908ba6c00a3f17317_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{n=1}^\infty n \cdot b_{i,n} = \binom{0}{i-1} \cdot {_2F_1}(1,-i,2-i;-1).\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-0f3dccf6f75fd13139f30b246197f5bb_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{i=1}^n b_{i,n} = \frac{1}{2}\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-96db9a287f5e5379a366181fa278d0e1_l3.png)
![Rendered by QuickLaTeX.com \[\frac{1}{\sqrt{2\pi(n-1)}}e^{-\frac{(i - n/2 - 1/2)^2}{(n - 1)/2}.\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-a116c9ac4435931ac0b441c0a434f974_l3.png)
![Rendered by QuickLaTeX.com \[\begin{aligned} b_{i,n} &=a_{i,n-1} - a_{i,n} \\ &= \frac{1}{2}(a_{i-1,n-2}+a_{i,n-2}-a_{i,n-1}-a_{i-1,n-1}) \\ &= \frac{b_{i,n-1}+b_{i-1,n-1}}{2}.\end{aligned}\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-da6343d9bf534f13b5dc03dfc1a22bc1_l3.png)
 . For player i to die on step n, the previous i – 1 players must have died somewhere amongst the n – 1 prior steps. There are “n – 1 choose i – 1″ ways to arrange these mistaken steps, out of
. For player i to die on step n, the previous i – 1 players must have died somewhere amongst the n – 1 prior steps. There are “n – 1 choose i – 1″ ways to arrange these mistaken steps, out of ![Rendered by QuickLaTeX.com \[b_{i,n} := P(i\textrm{ dies on }n) = \binom{n-1}{i-1}2^{-n}.\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-aacd3fe49ce5a0492c0f36aef8ec97da_l3.png)
![Rendered by QuickLaTeX.com \[P(i\textrm{ players died by }n) = \binom{n}{i}2^{-n}.\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-6d44375f1554e6a734df81effcf84eb8_l3.png)
![Rendered by QuickLaTeX.com \[P(i,n) = 1-\binom{n}{i}2^{-n}\cdot{_2F_1}(1,i-n,i+1;-1).\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-c2a20461aa048defc051d32943dbc8a9_l3.png)

![Rendered by QuickLaTeX.com \[a_{i,n} = a_{i-1,n-1} + \sum_{k=1}^{n-1} ( a_{i-1,k-1} - a_{i-1,k} ) / 2^{n-k}.\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-4d627692bbc0347df278931cf76ca111_l3.png)
![Rendered by QuickLaTeX.com \[g'^{\mu\nu} = \begin{pmatrix} -1 & -u^1 & -u^2 & -u^3 \\ -u^1 & g^{11} & g^{12} & g^{13} \\ -u^2 & g^{21} & g^{22} & g^{23} \\ -u^3 & g^{31} & g^{32} & g^{33} \end{pmatrix}.\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-f2de30201432026fda1960ec99333f55_l3.png)