Black hole spacetimes – CMacLaurin.com

(Poster) Static vs Falling: Time slicings of Schwarzschild black holes

I presented this poster, “Static vs Falling: Time slicings of Schwarzschild black holes” at the GR21 conference in New York City, July 2016. You can download a PDF version. A big thank-you to those who gave feedback, especially to Jiří Podolský who encouraged me to publish it! The section on coordinate vectors has been updated. Also there is a major update to the poster. Schwarzschild slicings 40dpi

Tetrad for Schwarzschild metric, in terms of e

The following is a natural choice of orthonormal tetrad for an observer moving radially in Schwarzschild spacetime with “energy per unit rest mass” e:

$\begin{align*} e_{\hat 0}^\mu &= \left(e\Schw^{-1},\pm\eroot,0,0\right) \\ e_{\hat 1}^\mu &= \left(\pm\Schw^{-1}\eroot,e,0,0\right) \\ e_{\hat 2}^\mu &= \left(0,0,\frac{1}{r},0\right) \\ e_{\hat 3}^\mu &= \left(0,0,0,\frac{1}{r\sin\theta}\right) \end{align*}$

The components are given in Schwarzschild coordinates. (The ± signs are not independent — they must be either both +1 or both -1. Note that e does not distinguish between inward and outward motion. There is additional freedom to define any of these vectors as their negative.)

We normally think of e as invariant, where there is a presumption of freely falling / geodesic motion, but even if not we can regard it as an instantaneous value.

$\evec{0}$ is the 4-velocity computed previously. The other vectors can be obtained from substituting $\gamma=e\Schw^{-1/2}$ and $V=-\frac{1}{e}\sqrt{e^2-1+\frac{2M}{r}}$ into the tetrad here. $\gamma$ is determined from $-\fvec u\cdot\fvec u_{\rm obs}=\gamma$ and the equation for e above, then V follows from inverting $\gamma\equiv(1-V^2)^{-1/2}$ . This orthonormal frame is useful for determining the object’s perspective, e.g. tidal forces, visual appearances, etc.

Tetrad for Schwarzschild metric

Suppose an observer u moves radially with speed (3-velocity) $V$ relative to “stationary” Schwarzschild observers, where we define $V<0$ as inward motion. Then one natural choice of orthonormal tetrad is:

$\begin{align*} (\evec{0})^\alpha &= \left(\gamma\Schw^{-1/2},V\gamma\Schw^{1/2},0,0\right) \\ (\evec{1})^\alpha &= \left(V\gamma\Schw^{-1/2},\gamma\Schw^{1/2},0,0\right) \\ (\evec{2})^\alpha &= \left(0,0,\frac{1}{r},0\right) \\ (\evec{3})^\alpha &= \left(0,0,0,\frac{1}{r\sin\theta}\right) \end{align*}$

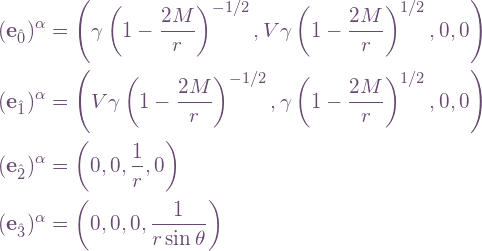
where the components are given in Schwarzschild coordinates. This may be derived as follows.

The Schwarzschild observer has 4-velocity

$\fvec u_{\rm obs}=\left(\Schw^{-1/2},0,0,0\right)$

because the spatial coordinates are fixed, and the t-component follows from normalisation $\fvec u_{\rm obs}\cdot\fvec u_{\rm obs}=-1$ (Hartle textbook §9.2).

Now the Lorentz factor for the relative speed satisfies $-\fvec u\cdot\fvec u_{\rm obs}=\gamma$ , and together with normalisation $\fvec u\cdot\fvec u=-1$ and the assumption that the θ and φ components are zero, this yields $\evec{0}\equiv\fvec u$ given above.

We obtain $\evec{1}$ by orthonormality: $\evec{1}\cdot\evec{0}=0$ and $\evec{1}\cdot\evec{1}=1$ , and again making the assumption the θ and φ components are zero. Note the negative of the r-component is probably an equally natural choice. Then $\evec{2}$ and $\evec{3}$ follow from simply normalising the coordinate vectors.

Strictly speaking this setup only applies for $r>2M$ , because stationary timelike observers cannot exist inside a black hole event horizon! Yet remarkably the formulae can work out anyway (MTW textbook …) . An alternate approach is local Lorentz boost described shortly.

Hartle textbook … Also check no “twisting” etc…

Radial motion in the Schwarzschild metric, in terms of e

A nice way to parametrise the 4-velocity u of a small test body moving radially within Schwarzschild spacetime is by the “energy per unit rest mass” e:

${u^\mu=\left(e\Schw^{-1},\pm\eroot,0,0\right)$

For the “±” term, choose the sign based on whether the motion is inwards or outwards. All components are given in Schwarzschild coordinates $(t,r,\theta,\phi)$ . The result was derived as follows. In geometric units, the metric is:

$\Schwmetric$

By definition $e\equiv-\fvec\xi\cdot\fvec u$ , where $\fvec\xi\equiv\partial_t$ is the Killing vector corresponding to the independence of the metric from t, and has components $\xi^\mu=(1,0,0,0)$ (Hartle textbook §9.3). For geodesic (freefalling) motion e is invariant, however even for accelerated motion e is well-defined instantaneously and makes a useful parametrisation.

We want to find $u^\mu=(u^t,u^r,u^\theta,u^\phi)$ say. Rearranging the defining equation for e gives $u^t=e\Schw^{-1}$ . Radial motion means $u^\theta=u^\phi=0$ , so the normalised condition $\fvec u\cdot\fvec u=-1$ yields the remaining component $\abs{u^r}$ . The resulting formula is valid for all $0<r\ne 2M$ , and for e=1 the 4-velocity describes “raindrops” as expected.