Tag: Lorentz boost

Tetrad for Schwarzschild metric

Suppose an observer u moves radially with speed (3-velocity) V relative to “stationary” Schwarzschild observers, where we define V<0 as inward motion. Then one natural choice of orthonormal tetrad is:

    \begin{align*} (\evec{0})^\alpha &= \left(\gamma\Schw^{-1/2},V\gamma\Schw^{1/2},0,0\right) \\ (\evec{1})^\alpha &= \left(V\gamma\Schw^{-1/2},\gamma\Schw^{1/2},0,0\right) \\ (\evec{2})^\alpha &= \left(0,0,\frac{1}{r},0\right) \\ (\evec{3})^\alpha &= \left(0,0,0,\frac{1}{r\sin\theta}\right) \end{align*}

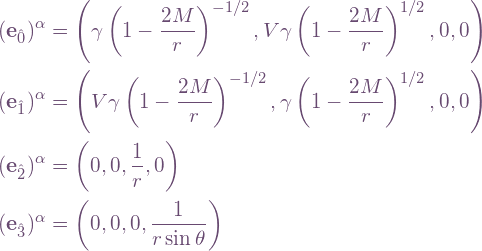
where the components are given in Schwarzschild coordinates. This may be derived as follows.

The Schwarzschild observer has 4-velocity

    \[\fvec u_{\rm obs}=\left(\Schw^{-1/2},0,0,0\right)\]

because the spatial coordinates are fixed, and the t-component follows from normalisation \fvec u_{\rm obs}\cdot\fvec u_{\rm obs}=-1 (Hartle §9.2).

Now the Lorentz factor for the relative speed satisfies -\fvec u\cdot\fvec u_{\rm obs}=\gamma, and together with normalisation \fvec u\cdot\fvec u=-1 and the assumption that the θ and φ components are zero, this yields \evec{0}\equiv\fvec u given above.

We obtain \evec{1} by orthonormality: \evec{1}\cdot\evec{0}=0 and \evec{1}\cdot\evec{1}=1, and again making the assumption the θ and φ components are zero. Note the negative of the r-component is probably an equally natural choice. Then \evec{2} and \evec{3} follow from simply normalising the coordinate vectors.

Strictly speaking this setup only applies for r>2M, because stationary timelike observers cannot exist inside a black hole event horizon! Yet remarkably the formulae can work out anyway (MTW …) .  An alternate approach is local Lorentz boost described shortly.

Hartle … Also check no “twisting” etc…