The following is a natural choice of orthonormal tetrad for an observer moving radially in Schwarzschild spacetime with “energy per unit rest mass” e:

The components are given in Schwarzschild coordinates. (The ± signs are not independent — they must be either both +1 or both -1. Note that e does not distinguish between inward and outward motion. There is additional freedom to define any of these vectors as their negative.)
We normally think of e as invariant, where there is a presumption of freely falling / geodesic motion, but even if not we can regard it as an instantaneous value.
![]() is the 4-velocity computed previously. The other vectors can be obtained from substituting
is the 4-velocity computed previously. The other vectors can be obtained from substituting ![]() and
and ![]() into the tetrad here.
into the tetrad here. ![]() is determined from
is determined from ![]() and the equation for e above, then V follows from inverting
and the equation for e above, then V follows from inverting ![]() . This orthonormal frame is useful for determining the object’s perspective, e.g. tidal forces, visual appearances, etc.
. This orthonormal frame is useful for determining the object’s perspective, e.g. tidal forces, visual appearances, etc.
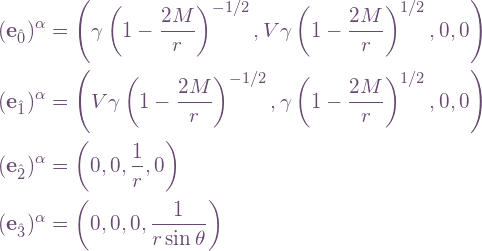
![Rendered by QuickLaTeX.com \[\fvec u_{\rm obs}=\left(\Schw^{-1/2},0,0,0\right)\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-492ec50d4e2d8170e1f27d344d1d02ba_l3.png)
 §9.2).
§9.2).![Rendered by QuickLaTeX.com \[{u^\mu=\left(e\Schw^{-1},\pm\eroot,0,0\right)\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-18f14260dbcfd3c0686a273a72319a5c_l3.png)
![Rendered by QuickLaTeX.com \[\Schwmetric\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-c9af12fa8aa92d2f1d3a9a32b73b81fc_l3.png)