tetrad – CMacLaurin.com

Suppose an observer u moves radially with speed (3-velocity) $V$ relative to “stationary” Schwarzschild observers, where we define $V<0$ as inward motion. Then one natural choice of orthonormal tetrad is:

$\begin{align*} (\evec{0})^\alpha &= \left(\gamma\Schw^{-1/2},V\gamma\Schw^{1/2},0,0\right) \\ (\evec{1})^\alpha &= \left(V\gamma\Schw^{-1/2},\gamma\Schw^{1/2},0,0\right) \\ (\evec{2})^\alpha &= \left(0,0,\frac{1}{r},0\right) \\ (\evec{3})^\alpha &= \left(0,0,0,\frac{1}{r\sin\theta}\right) \end{align*}$

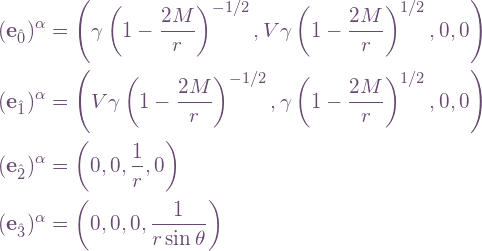
where the components are given in Schwarzschild coordinates. This may be derived as follows.

The Schwarzschild observer has 4-velocity

$\fvec u_{\rm obs}=\left(\Schw^{-1/2},0,0,0\right)$

because the spatial coordinates are fixed, and the t-component follows from normalisation $\fvec u_{\rm obs}\cdot\fvec u_{\rm obs}=-1$ (Hartle textbook §9.2).

Now the Lorentz factor for the relative speed satisfies $-\fvec u\cdot\fvec u_{\rm obs}=\gamma$ , and together with normalisation $\fvec u\cdot\fvec u=-1$ and the assumption that the θ and φ components are zero, this yields $\evec{0}\equiv\fvec u$ given above.

We obtain $\evec{1}$ by orthonormality: $\evec{1}\cdot\evec{0}=0$ and $\evec{1}\cdot\evec{1}=1$ , and again making the assumption the θ and φ components are zero. Note the negative of the r-component is probably an equally natural choice. Then $\evec{2}$ and $\evec{3}$ follow from simply normalising the coordinate vectors.

Strictly speaking this setup only applies for $r>2M$ , because stationary timelike observers cannot exist inside a black hole event horizon! Yet remarkably the formulae can work out anyway (MTW textbook …) . An alternate approach is local Lorentz boost described shortly.

Hartle textbook … Also check no “twisting” etc…

Tag: tetrad

Tetrad for Schwarzschild metric