Last time we derived the 4-velocity u of a small test body moving radially in the Schwarzschild geometry, in terms of e, the “energy per unit rest mass”. Another parametrisation is in terms of the 3-speed V relative to stationary observers. This turns out to be, in Schwarzschild coordinate expression,
![Rendered by QuickLaTeX.com \[u^\mu=\left(\gamma\Schw^{-1/2},V\gamma\Schw^{1/2},0,0\right)\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-48c3e5c70843e13b1e6957f2601ceb0b_l3.png)
To derive this, first consider the 4-velocity of stationary observers:
![Rendered by QuickLaTeX.com \[u_{\rm{Schw}}^\mu=\left(\Schw^{-1/2},0,0,0\right)\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-c4a86d1b00b5ddd39fca03808b1d8751_l3.png)
We know the “moving” body has 4-velocity u of form 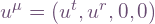 since the motion is radial. The Lorentz factor
since the motion is radial. The Lorentz factor  for the relative speed is
for the relative speed is
![Rendered by QuickLaTeX.com \[\gamma=-\fvec u\cdot\fvec u_{\rm{Schw}}\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-0f209dd4ca28eef7c46c36eade5c9982_l3.png)
Evaluating and rearranging yields  . Normalisation
. Normalisation 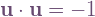 leads to
leads to  , after some algebra including use of the identity
, after some algebra including use of the identity  . We allow
. We allow  also, and define this as inward motion. Carefully considering the sign, this results in the top equation. (An alternate derivation is to perform a local Lorentz boost. Later articles will discuss this… The Special Relativity formulae cannot be applied directly to Schwarzschild coordinates.)
also, and define this as inward motion. Carefully considering the sign, this results in the top equation. (An alternate derivation is to perform a local Lorentz boost. Later articles will discuss this… The Special Relativity formulae cannot be applied directly to Schwarzschild coordinates.)
Some special cases are noteworthy. For V=0, γ=1, and u reduces to uSchw. This corresponds to 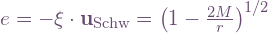 . Also we can relate the parametrisation by V (and γ) to the parametrisation by e via
. Also we can relate the parametrisation by V (and γ) to the parametrisation by e via
![Rendered by QuickLaTeX.com \[\gamma=e\Schw^{-1/2}\qquad V=-\frac{1}{e}\sqrt{e^2-1+\frac{2M}{r}}\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-a90b1978322ac54ce4c637445bc77fed_l3.png)
where the leftmost equation follows from the definition  , and subsequently the rightmost equation from γ=γ(V). For raindrops with e=1, the relative speed reduces to
, and subsequently the rightmost equation from γ=γ(V). For raindrops with e=1, the relative speed reduces to 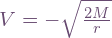 .
.
We would expect the construction to fail for 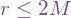 , as stationary timelike observers cannot exist there, and so the relative speed to them would become meaningless. But curiously, it can actually work for a faster-than-light V>1 “Lorentz” boost, as even the authorities MTW
, as stationary timelike observers cannot exist there, and so the relative speed to them would become meaningless. But curiously, it can actually work for a faster-than-light V>1 “Lorentz” boost, as even the authorities MTW  (§31.2, explicit acknowledgement) and Taylor & Wheeler
(§31.2, explicit acknowledgement) and Taylor & Wheeler  (§B.4, implicitly vrel>1 for r<2M) attest. Sometime, I will investigate this further…
(§B.4, implicitly vrel>1 for r<2M) attest. Sometime, I will investigate this further…
![]()
![]()
![]()
![]() , then multiply both sides by γ2 and rearrange.
, then multiply both sides by γ2 and rearrange.![Rendered by QuickLaTeX.com \[u^\mu=\left(\gamma\Schw^{-1/2},V\gamma\Schw^{1/2},0,0\right)\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-48c3e5c70843e13b1e6957f2601ceb0b_l3.png)
![Rendered by QuickLaTeX.com \[u_{\rm{Schw}}^\mu=\left(\Schw^{-1/2},0,0,0\right)\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-c4a86d1b00b5ddd39fca03808b1d8751_l3.png)
![Rendered by QuickLaTeX.com \[\gamma=e\Schw^{-1/2}\qquad V=-\frac{1}{e}\sqrt{e^2-1+\frac{2M}{r}}\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-a90b1978322ac54ce4c637445bc77fed_l3.png)
 (§31.2, explicit acknowledgement) and
(§31.2, explicit acknowledgement) and ![Rendered by QuickLaTeX.com \[{u^\mu=\left(e\Schw^{-1},\pm\eroot,0,0\right)\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-18f14260dbcfd3c0686a273a72319a5c_l3.png)
![Rendered by QuickLaTeX.com \[\Schwmetric\]](http://cmaclaurin.com/cosmos/wp-content/ql-cache/quicklatex.com-c9af12fa8aa92d2f1d3a9a32b73b81fc_l3.png)